在算法竞赛中，经常需要测试自己写的程序，这时候就少不了会用到取随机数的函数rand()来生成随机数。看算法书的时候，里面说srand()函数只需在程序开头调用一次，我不是很理解，于是有了这篇文章。

取随机数的基本使用

rand()函数

rand()函数是 C++ 标准库<cstdlib>中的一部分，它的作用是生成一个伪随机整数。伪随机数的特点是，它们看似随机，但实际上是基于一个确定性的算法生成的。如果不加以干预，每次运行程序时，rand()函数会生成相同的随机数序列。

rand()的函数原型如下：

int rand();

这个函数不需要任何参数，返回值是int型，具体返回值范围为[0, RAND_MAX]，其中RAND_MAX是一个在<cstdlib>中定义的一个常量，其值至少为32767（即十六进制数0x7fff）。

以下代码演示了如何使用rand()函数生成一个随机数：

#include <iostream>
#include <cstdlib>
using namespace std;

int main() {
    int randomNumber = rand();
    cout << "Random number: " << randomNumber << endl;
    return 0;
}

运行这段代码，你会发现每次运行程序时，输出的随机数都是相同的。这是因为rand函数在生成随机数时，依赖于一个内部的种子值。如果没有显式地设置种子值，rand()函数会使用默认的种子值，从而导致每次生成的随机数序列相同。

srand()函数

为了让rand()函数生成不同的随机数序列，我们需要使用srand()函数来设置随机数种子。srand()函数也是<cstdlib>库的一部分，其原型如下：

void srand(unsigned int seed);

srand()函数接受一个无符号整数unsigned int作为参数，这个参数就是随机数种子。种子值决定了rand()函数生成的随机数序列。如果两次运行程序时，srand()函数使用相同的种子值，那么rand()函数将生成相同的随机数序列。

例如这个例子：

#include <iostream>
#include <cstdlib>
using namespace std;

int main() {
    srand(123); // 设置种子值为123
    for (int i = 0; i < 5; ++i) {
        int randomNumber = rand();
        cout << "Random number: " << randomNumber << endl;
    }
    return 0;
}

我们设置了123作为种子值，每次运行程序时，rand()函数都会从这个固定的种子值开始生成随机数，因此每次输出的随机数序列都是相同的。就像上面的程序一样，每次运行，连续使用rand()函数获得的5个值都和之前运行的一样。

使用时间作为种子值

为了让每次运行程序时生成的随机数序列都不同，我们通常使用当前时间作为srand()函数的种子值。因为时间是不断变化的，每次运行程序时的时间都不同，所以使用时间作为种子值可以确保每次生成的随机数序列都是不同的。

在 C++ 中，我们可以使用<ctime>库中的time()函数来获取当前时间。time()函数的原型如下：

time_t time(time_t* timer);

该函数接收一个time_t类型的指针作为参数（这个参数可以为nullptr，即一个空指针），并返回一个time_t类型的值。time_t类型其实就是int64型（即long long型），该类型的定义在corecrt.h和_mingw.h中。

// <corecrt.h>
__MINGW_EXTENSION typedef __int64 __time64_t;

// <_mingw.h>
#define __int64 long long

该函数返回自 1970 年 1 月 1 日 00:00:00 以来经过的秒数。如果timer参数不为空，time()函数还会将返回值存储到timer指向的变量中。

通常，我们可以显式地将time()函数的返回值强制转换为unsigned int类型，并作为srand()函数的参数，如下所示：

#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;

int main() {
    srand(static_cast<unsigned int>(time(nullptr))); // 使用当前时间作为种子值
    for (int i = 0; i < 5; ++i) {
        int randomNumber = rand();
        cout << "Random number: " << randomNumber << endl;
    }
    return 0;
}

在上述代码中，我们通过static_cast<unsigned int>(time(nullptr))将time()函数返回的time_t类型值（即long long）转换为unsigned int类型，并作为srand()函数的参数。这样，每次运行程序时，srand()函数都会使用不同的种子值，从而使rand()函数生成不同的随机数序列。

为什么srand()只在开头调用一次

来看一个这样的程序：

#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;

int main() {
    for (int i = 0; i < 5; ++i) {
        srand(static_cast<unsigned int>(time(nullptr))); // 使用当前时间作为种子值
        int randomNumber = rand();
        cout << "[" << i << "] Random number: " << randomNumber << endl;
    }
    return 0;
}

咋一看，这个程序应该会生成5个不同的随机数才对，但实际运行结果却是这样的：

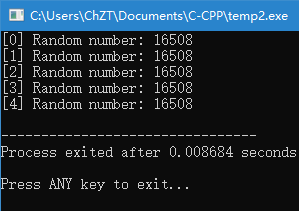
程序输出了5个相同的数。这一现象看似违背常理，毕竟我们期望通过srand(static_cast<unsigned int>(time(nullptr)))来利用系统时间的变化获取不同的随机数种子。但事实上问题就出现在这里，time()函数返回的是自 1970 年 1 月 1 日 00:00:00 以来经过的秒数，而for循环的执行速度实在是太快了，循环内的每次迭代所花费的时间极短，远远小于 1 秒。这就导致在循环的多次迭代过程中，time()函数返回的秒数在绝大多数情况下是相同的。由于srand()函数依据传入的种子值来初始化随机数生成器，当每次循环中srand(static_cast<unsigned int>(time(nullptr)))接收到的种子值相同时，随机数生成器就会被初始化为相同的状态。

例如，假设在某一时刻开始执行for循环，此时time()函数返回的值为1672531200，在循环的前几百次甚至上千次迭代中，time()函数可能仍然返回1672531200，因为循环执行的时间跨度未超过 1 秒。这样一来，每次调用srand()时，随机数生成器都被设置为相同的初始状态，后续调用rand()函数生成的随机数自然也就相同了。

我们可以写一个程序来验证一下这个：

#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;

int main() {
	time_t cur_time;
	for (int i = 0; i < 5; ++i) {
		srand(static_cast<unsigned int>(time(&cur_time))); // 使用当前时间作为种子值
		int randomNumber = rand();
		cout << "[" << cur_time << "] Random number: " << randomNumber << endl;
	}
	return 0;
}

运行结果如下：

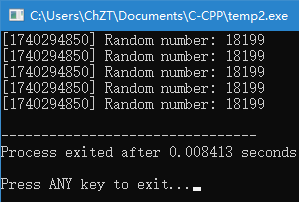
可以看到在循环中获得到的时间确实是一样的。

接下来我们在每次循环中添加一个延时500毫秒（即0.5秒）的语句看看：

#include <iostream>
#include <cstdlib>
#include <ctime>
#include <windows.h>
using namespace std;

int main() {
	time_t cur_time;
	for (int i = 0; i < 5; ++i) {
		srand(static_cast<unsigned int>(time(&cur_time))); // 使用当前时间作为种子值
		int randomNumber = rand();
		cout << "[" << cur_time << "] Random number: " << randomNumber << endl;
		Sleep(500);		// 延时500ms，该函数在头文件 windows.h 中
	}
	return 0;
}

运行结果如下：

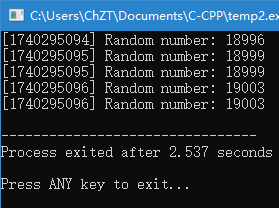
可以看到由于获取到的时间不同，获得的随机数也不一样了。

rand()取随机数的原理

在上一个程序中，我们如果把代码中的循环次数从5次变成50次，再看运行结果：

[1740295268] Random number: 19564
[1740295269] Random number: 19568
[1740295269] Random number: 19568
[1740295270] Random number: 19571
[1740295270] Random number: 19571
[1740295271] Random number: 19574
[1740295271] Random number: 19574
[1740295272] Random number: 19577
[1740295272] Random number: 19577
[1740295273] Random number: 19581
[1740295273] Random number: 19581
[1740295274] Random number: 19584
[1740295274] Random number: 19584
[1740295275] Random number: 19587
[1740295275] Random number: 19587
[1740295276] Random number: 19590
[1740295276] Random number: 19590
[1740295277] Random number: 19594
[1740295277] Random number: 19594
[1740295278] Random number: 19597
[1740295278] Random number: 19597
[1740295279] Random number: 19600
[1740295279] Random number: 19600
[1740295280] Random number: 19603
[1740295280] Random number: 19603
[1740295281] Random number: 19607
[1740295281] Random number: 19607
[1740295282] Random number: 19610
[1740295282] Random number: 19610
[1740295283] Random number: 19613
[1740295283] Random number: 19613
[1740295284] Random number: 19617
[1740295284] Random number: 19617
[1740295285] Random number: 19620
[1740295285] Random number: 19620
[1740295286] Random number: 19623
[1740295287] Random number: 19626
[1740295287] Random number: 19626
[1740295288] Random number: 19630
[1740295288] Random number: 19630
[1740295289] Random number: 19633
[1740295289] Random number: 19633
[1740295290] Random number: 19636
[1740295290] Random number: 19636
[1740295291] Random number: 19639
[1740295291] Random number: 19639
[1740295292] Random number: 19643
[1740295292] Random number: 19643
[1740295293] Random number: 19646
[1740295293] Random number: 19646

可以发现，取随机数的结果有了一定的规律。要想知道原因，就得知道rand()函数取随机数的原理了。

具体来说，rand()函数通常使用线性同余法（Linear Congruential Generator, LCG）来生成伪随机数。线性同余法的公式如下：

$X_{n + 1} = (aX_n + c) \bmod m$

其中：

•  $X_n$是当前的随机数生成器状态（也称为种子值）。
•  $a$是乘数。
•  $c$是增量。
•  $m$是模数。
•  $X_{n + 1}$是下一个随机数生成器状态。

每次调用 rand() 函数时，它会根据当前的$X_n$值，使用上述公式计算出$X_{n+1}$，并将$X_{n+1}$作为下一次调用 rand() 函数时的种子值。同时，rand() 函数会返回一个基于$X_{n+1}$的伪随机整数。

由于使用了有规律的数值作为种子值，所以取到的随机数也仍然会呈现出一定的规律性。

所以，一般srand()函数只需要在程序最开头调用一次，而不是在循环中重复调用。