在一些数学公式的推导中,常会遇到 𝑑 / 𝜕 / 𝛿 \ Δ 等符号。它们背后分别代表的数学含义?
增量
设变量 𝑢 从它的一个初值 𝑢1 变到终值 𝑢2,终值与初值的差 𝑢2−𝑢1 就叫做变量 𝑢 的增量,记作 Δ𝑢,即Δ𝑢=𝑢2−𝑢1
增量 Δ𝑢 可以是正的,也可以是负的。
应该注意到:记号 Δ𝑢 并不表示某个量 Δ 与变量 𝑢 的乘积,而是一个整体不可分割的记号。
举例:
现在假定函数 𝑦=𝑓(𝑥) 在点 𝑥0 的某一个邻域内是有定义的。当自变量 𝑥 在这个邻域内从 𝑥0 变到 𝑥0+Δ𝑥 时,函数值(或因变量) 𝑓(𝑥) 相应地从 𝑓(𝑥0) 变到 𝑓(𝑥0+Δ𝑥),因此,函数值(或因变量) 𝑓(𝑥) 的对应增量为Δ𝑦=𝑓(𝑥0+Δ𝑥)−𝑓(𝑥0)
习惯上也称 Δ𝑦 为函数的增量。
由此,可以定义函数的连续性,如下:
设函数 𝑦=𝑓(𝑥) 在点 𝑥0) 的某一个邻域内有定义,如果,limΔ𝑥→0Δ𝑦=limΔ𝑥→0[𝑓(𝑥0+Δ𝑥)−𝑓(𝑥0)]=0,
那么就称函数 𝑦=𝑓(𝑥) 在点 𝑥0 连续。
导数
导数的定义: 设函数 𝑦=𝑓(𝑥) 在点 𝑥0 的某个邻域内有定义,当自变量 𝑥 在 𝑥0 处取得增量 Δ𝑥 (点 𝑥0+Δ𝑥 仍在该邻域内)时,相应地,因变量取得增量 Δ𝑦=𝑓(𝑥0+Δ𝑥)−𝑓(𝑥0);如果 Δ𝑦 与 Δ𝑥 之比当 Δ𝑥→0 时的极限存在,那么称函数 𝑦=𝑓(𝑥) 在点 𝑥0 处可导,并称这个极限为函数 𝑦=𝑓(𝑥) 在点 𝑥0 处的导数,记为 𝑓′(𝑥) ,即𝑓′(𝑥)=limΔ𝑥→0Δ𝑦Δ𝑥=limΔ𝑥→0𝑓(𝑥0+Δ𝑥)−𝑓(𝑥0)Δ𝑥,
也可记作 𝑦′|𝑥=𝑥0,$$\frac{dy}{dx}|_{x = x_0}$ 或 𝑑𝑓(𝑥)𝑑𝑥|𝑥=𝑥0。
可以看出,导数等于 增量 Δ𝑦 和增量 Δ𝑥 比值的极限。
函数的微分
微分的定义: 设函数 𝑦=𝑓(𝑥) 在某区间内有定义,𝑥0 及 𝑥0+Δ𝑥 在这个区间内,如果函数的增量Δ𝑦=𝑓(𝑥0+Δ𝑥)−𝑓(𝑥0)
可表示为Δ𝑦=𝐴Δ𝑥+𝑜(Δ𝑥)
其中,𝐴 是不依赖于 Δ𝑥 的常数,那么,称函数 𝑦=𝑓(𝑥) 在点 𝑥0 是可微的,而 𝐴Δ𝑥 叫做函数 𝑦=𝑓(𝑥) 在点 𝑥0 相应于自变量增量 Δ𝑥 的微分,即𝑑𝑦=𝐴Δ𝑥
注: 函数 𝑓(𝑥) 在点 𝑥0 可微的充要条件是函数 𝑓(𝑥) 在点 𝑥0 可导。
微分的意思是指,因变量的增量 Δ𝑦,是自变量的增量 Δ𝑥 的线性函数,且记作 𝑑𝑦。所以说,应该有如下关系:
增量 Δ𝑦 是实实在在、真实的变化值。只是,只有当可导的时候,才能写成 Δ𝑦=𝐴Δ𝑥+𝑜(Δ𝑥)=𝑑𝑦+𝑜(Δ𝑥)=𝑑𝑦+𝑜(𝑑𝑦) 。也就是说,微分,只是增量 Δ𝑦 的一个近似值。
另外一点,在定义导数的时候,也是用增量 Δ𝑦 与 Δ𝑥 的比值来定义的,并不是用微分。只是,导数的值,刚好等于微分 𝑑𝑦 与 𝑑𝑥 的比值。
注二: 通常把自变量 𝑥 的增量 Δ𝑥 称为自变量的微分,记作 𝑑𝑥,即 𝑑𝑥=Δ𝑥。于是,函数 𝑦=𝑓(𝑥) 的微分又可记作为𝑑𝑦=𝑓′(𝑥)𝑑𝑥
从而有𝑑𝑦𝑑𝑥=𝑓′(𝑥)
这就是说,函数的微分 𝑑𝑦 与自变量的微分 𝑑𝑥 之商等于该函数的导数,因此,导数也叫作“微商”。
微分的几何意义
如下图所示,自变量的增量为 Δ𝑥=𝑃𝑅 ,因变量的增量为 Δ𝑦=𝑅𝑄 。那么,在 𝑥0 点作曲线的切线,则得到函数 𝑦=𝑓(𝑥) 在点 𝑥0 相应于自变量增量 Δ𝑥 的微分 𝑑𝑦=𝑅𝑄′ 。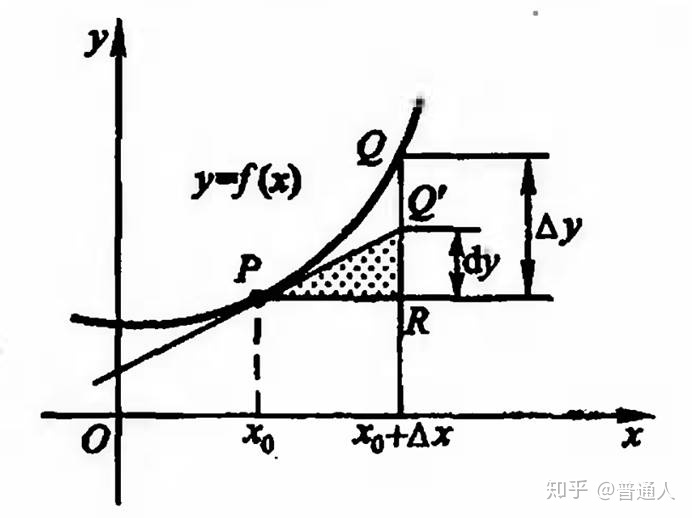
由此可见,对于可微函数 𝑦=𝑓(𝑥) 而言,当 Δ𝑦 是曲线 𝑦=𝑓(𝑥) 上的点的纵坐标的增量时,𝑑𝑦 就是曲线的切线上点的纵坐标的相应增量。
只是,当 |Δ𝑥| 很小时,比|Δ𝑦−𝑑𝑦|比|\Delta x| 小得多。因此,在点 M 的邻近,我们可以用切线段来近似代替曲线段。在局部范围内用线性函数近似代替非线性函数,在几何上就是局部用切线段近似代替曲线段。这在数学上称为非线性函数的局部线性化,这是微分学的基本思想之一。
基本初等函数的微分公式与微分运算法则
从函数的微分表达式𝑑𝑦=𝑓′(𝑥)𝑑𝑥
可以看出,要计算函数的微分,只要计算函数的导数,再乘自变量的微分。那么,可得到如下的微分公式和微分运算法则:
(略)
偏导数
偏导数的定义: 设函数 𝑧=𝑓(𝑥,𝑦) 在点 (𝑥0,𝑦0) 的某一邻域内有定义,当 𝑦 固定在 𝑦0 而 𝑥 在 𝑥0 处有增量 Δ𝑥 时,相应的函数有增量𝑓(𝑥0+𝑥,𝑦0)−𝑓(𝑥0,𝑦0)
如果limΔ𝑥→0𝑓(𝑥0+Δ𝑥,𝑦0)−𝑓(𝑥0,𝑦0)Δ𝑥
存在,那么称此极限为函数 𝑧=𝑓(𝑥,𝑦) 在点 (𝑥0,𝑦0) 处对 𝑥 的偏导数,记作𝜕𝑧𝜕𝑥|𝑥=𝑥0𝑦=𝑦0,
如果函数 𝑧=𝑓(𝑥,𝑦) 在区域 𝐷 内每一个点 (𝑥,𝑦) 处对 𝑥 的偏导数都存在,那么这个偏导数就是 𝑥,𝑦 的函数,它就称为函数 𝑧=𝑓(𝑥,𝑦) 对自变量 𝑥 的偏导函数,记作或𝜕𝑧𝜕𝑥,𝜕𝑓𝜕𝑥,或𝑓𝑥(𝑥,𝑦)
类似地,可以定义函数 𝑧=𝑓(𝑥,𝑦) 对自变量 𝑦 的偏导函数,记作或𝜕𝑧𝜕𝑦,𝜕𝑓𝜕𝑦,或𝑓𝑦(𝑥,𝑦)
注:偏导数仍然是增量的比值。
偏导数的几何意义:偏导数 𝑓𝑥(𝑥,𝑦) 的几何意义是曲面被平面 𝑦=𝑦0 所截得的曲线在点 𝑥0 处的斜率。
偏微分 / 全微分
根据一元函数微分学中增量与微分的关系,可得𝑓(𝑥+Δ𝑥,𝑦)−𝑓(𝑥,𝑦)≈𝑓𝑥(𝑥,𝑦)Δ𝑥,𝑓(𝑥,𝑦+Δ𝑦)−𝑓(𝑥,𝑦)≈𝑓𝑦(𝑥,𝑦)Δ𝑦,
上面两式的左端分别叫做二元函数对 𝑥 和对 𝑦 的偏增量,而右端分别叫做二元函数对 𝑥 和对 𝑦 的偏微分。
全增量: 设函数 𝑧=𝑓(𝑥,𝑦) 在点 𝑃(𝑥,𝑦) 的某个邻域内有定义,𝑃′(𝑥+Δ𝑥,𝑦+Δ𝑦) 为这个邻域内的任意一点,则称这两点的函数值之差 𝑓(𝑥+Δ𝑥,𝑦+Δ𝑦)−𝑓(𝑥,𝑦) 为函数在点 𝑃 对应于自变量增量 Δ𝑥 和 Δ𝑦 的全增量,记作 Δ𝑧 ,即Δ𝑧=𝑓(𝑥+Δ𝑥,𝑦+Δ𝑦)−𝑓(𝑥,𝑦)
注:一般来说,计算全增量 Δ𝑧 比较复杂。与一元函数的情形类似,我们希望用自变量的增量 Δ𝑥 和 Δ𝑦 的线性函数来近似地代替函数的全增量 Δ𝑧,从而引入如下定义:
全微分的定义: 设函数 𝑧=𝑓(𝑥,𝑦) 在点 (𝑥,𝑦) 的某个邻域内有定义,如果函数在点 (𝑥,𝑦) 的全增量Δ𝑧=𝑓(𝑥+Δ𝑥,𝑦+Δ𝑦)−𝑓(𝑥,𝑦)
可表示为Δ𝑧=𝐴Δ𝑥+𝐵Δ𝑦+𝑜(𝜌)
其中,𝐴 和 𝐵 不依赖于 Δ𝑥 和 Δ𝑦 而仅与 𝑥 和 𝑦 有关,𝜌=(Δ𝑥)2+(Δ𝑦)2,那么称函数 𝑧=𝑓(𝑥,𝑦) 在点 (𝑥,𝑦) 可微分,而 𝐴Δ𝑥+𝐵Δ𝑦 称为函数 𝑧=𝑓(𝑥,𝑦) 在点 (𝑥,𝑦) 的全微分,记作 𝑑𝑧 ,即𝑑𝑧=𝐴Δ𝑥+𝐵Δ𝑦
可微与可导的关系
定理1: 如果函数 𝑧=𝑓(𝑥,𝑦) 在点 (𝑥,𝑦) 可微分,那么该函数在点 (𝑥,𝑦) 的偏导数 𝜕𝑧𝜕𝑥 与 𝜕𝑧𝜕𝑦 必定存在,且函数 𝑧=𝑓(𝑥,𝑦) 在点 (𝑥,𝑦) 的全微分为𝑑𝑧=𝜕𝑧𝜕𝑥Δ𝑥+𝜕𝑧𝜕𝑦Δ𝑦
定理2: 如果函数𝑧=𝑓(𝑥,𝑦) 的偏导数 𝜕𝑧𝜕𝑥 与 𝜕𝑧𝜕𝑦 在点 (𝑥,𝑦) 连续,那么该函数在该点可微分。